• Macquarie Home »
• Faculty of Science »
• Physics and Astronomy »
• Astronomy

Age of a Planetary Nebula

Part 1: Measuring the Size of the Planetary Nebula

1. Open the image in IRIS.

   Select File » Load...
   Click on ngc3242-r.fit and then Open

   This should open the file but it will initially look all black. Click Auto in the Threshold window and you may also need to scroll down the image to see the PN (the PN is in the bottom half of the image). You can zoom in or out on your image using the zoom buttons: The left one zooms in, the middle one zooms out and the right one restores the image to its original size. The PN itself looks something like Figure 1, which has the important features marked.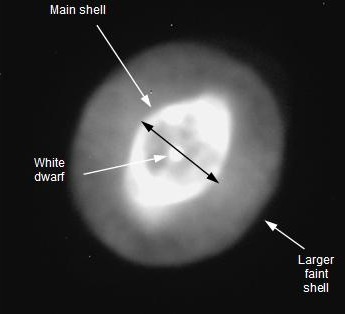

   
   Figure 1: The planetary nebula called the Ghost of Jupiter (NGC 3242).

   In the image you can see a bright central spot (the white dwarf) and a bright non-circular main shell surrounding the white dwarf. There is also a larger faint shell of gas visible which is probably gas that was lost by the star during its red giant phase.

2. Measure the edges of the main shell.

   You must decide where you think the edge of the main shell is. There may be significant differences depending on the threshold settings you have decided to use and this can be a topic for discussion in class: "How do you decide where the main shell finishes?"

   Select Analysis » Select Objects...

   If you get the error message Use x1 zoom, simply click on the x1 button alongside the zoom buttons described above to bring the image back to the original size.

   The cursor will change shape and an Output window will pop up on the screen. Click at one edge of the main shell and the x,y-coordinates will appear in the Output window. Click at the other edge of the shell and these x,y-coordinates will also appear in the Output window. A little + sign will show up where you have clicked. If you are not happy with your positions, you can click again. Just make sure you remember which were the correct measurements (see Figure 2).

   
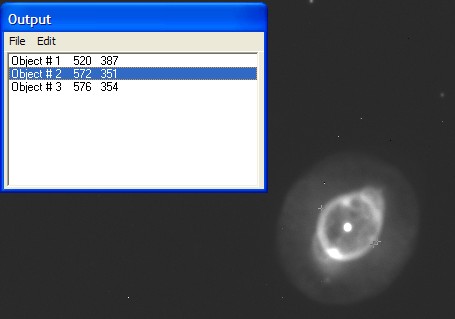
   Figure 2: Measurements of the edges of the main shell of the PN in the Output window. The second measurement didn't look to be in a good position (not right on the edge), so #1 and #3 will be used.

3. Determine the diameter of the shell in pixels.

   Using the Pythagorean theorem, these x,y positions can be used to determine the apparent diameter of the shell in pixels.

   Size in pixels = sqrt [(520 – 576)² + (387 – 354)²]
   = 65 pixels               

4. Determine the angular size of the main shell in arcseconds.

   Each pixel of the Faulkes Telescope images corresponds to a size of 0.27837 arcseconds. This is set by the properties of the CCD camera and the focal length of the telescope.

   Size in arcsec = 0.27837 arcsec/pixel * 65 pixels ≈ 18 arcsec

5. Find reference values for the expansion rate and the distance to the PN

   For this exercise, refer to: http://apod.nasa.gov/apod/ap051029.html and http://www.blackskies.org/pnweek4.htm and assume:

   • an expansion rate of v = 23 km/s; and
   • a distance of r = 1400 light years.
   Notes:
   • There are some assumptions made at this point. This exercise assumes that the shell of gas that defines the formation of the planetary nebula is the one that is indicated in the image as the main shell. It also assumes that the expansion velocity quoted in the reference is for the shell being measured.
   • These assumptions are complicated by the fact that this nebula is probably not spherical and it is hard to tell what shape it is. Many PN are shaped like an hourglass and there does appear to be some non-spherical shape in the image.
6. Determine the physical size of the PN using the small-angle formula

   The appendix, taken from this PDF document explains the derivation of the small-angle formula:

   l = r θ / 206165

   where l is the physical size, r is the distance (note that l and r must be expressed in like units — Mpc for galaxies, km for this exercise), θ is the angular size in arcseconds and 206265 is the number of arcseconds in a radian.

   Note: This simplifies to: l = r θ if the angle is measured in radians. You may see this version in some references (see Figure 3).

   
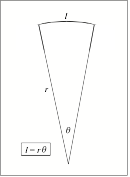
   Figure 3: Principles behind the small-angle formula. For very small angles:

   • l may be considered to be a straight line (forming a right-angled triangle); and
   • the tangent of an angle, where the angle is expressed in radians, is approximately equal to the angle itself.

   Follow these steps to calculate the physical size of NGC 3242:

   • Work out or look up how many kilometres in a light year.
   • Multiply this by the assumed distance to the PN (1400 l.y.) to find r in km.
   • The angle θ is the value found in Step 4 — note that this is in arcseconds.
   • Plug the numbers into the correct formula to derive the physical diameter l.

   Your answer should be of order 10¹² km.

Part 2: Calculating the Age

Return to the main page for this module